V nejjednodušším případě bude mapa jen obyčejná louka, bez jakýchkoli nástrah a překážek. Vaše družina se v takovém případě postupně přesune přímo k cíli po nejkratší možné cestě - přímce. Pro její výpočet může posloužit třeba Bresenhamův algoritmus (EN). Pokud by se na cestě přeci jen objevila nějaká překážka, hrdinové by se (pokud programátor při průchodu cesty nebude ignorovat neprůchodná místa) zastavili. Na další cestu by jim takto jednoduchý algoritmus zřejmě nestačil.

Na řešení těchto problémů existuje několik řešení - algoritmů. Mezi ty známější patří například Dijkstrův algoritmus. Zjednodušeně řečeno, hledání se šíří na všechny strany od počátečního bodu bez ohledu na to, kterým směrem je cíl. Tak prohledá daleko větší část mapy, než by prohledal, pokud by mířil alespoň přibližným směrem k cíli.

Zjednodušení vyhledávací oblasti⌗

Před samotným vyhledáváním je dobré si vyhledávací oblast trochu zjednodušit - rozdělit ji do menších celků. Nejjednodušší je použití čtverců tak, jak to vidíte na obrázkách výše. Krom toho se často využívají hexy (en) (kdo by neznal sérii HoMaM) nebo trojúhelníků. Je ale jen na vás, jaký tvar využijete.

Poznámka: Pro jakýkoliv tvar, do kterého se oblast zjednoduší se v angličtině užívá pojem node. V tomto článku budu krom toho používat také pojem pole, který bude znamenat to samé.

Technická poznámka: Díky rozdělení do čtverců - nodů, je velice jednoduché vytvořit 2D mapu z dlaždic (anglicky tiles). Postačí dvourozměrné pole.

Otevřený a uzavřený seznam⌗

Celý princip vyhledávacího algoritmu A* je založen na dvou seznamech - uzavřeném (anglicky closed list) a otevřeném (anglicky opened list). Do uzavřeného se ukládají už prozkoumané nody, ke kterým se už nebudeme vracet. Do otevřeného seznamu se vloží ta pole, která se ještě musí projít.

Ohodnocení⌗

Stejně jako v reálném světě i na herní mapě nebude všude stejný povrch. Můžou zde být potoky, písčité duny, silnice, neprostupná skaliska atd. Je jasné, že na silnici se nám půjde lépe a rychleji, než v potoku nebo po skalním masivu. Proto je dobré do mapy zavést ohodnocení jednotlivých políček. Čim lepší a rychlejší schůdnost, tím menší ohodnocení. Podle této analogie bude mít silnice ohodnocení nejmenší a skály největší. Vaše postavy si pak budou moci jednoduše vybrat cestu, která bude tvořená nody s nejmenším ohodnocením. Taková cesta pro ně bude nejrychlejší a nejsnazší.

V A* pathfindingu se na ohodnocení jednotlivých polí používá následující vzorec:

\[ F = H + G \]

• $ G $ je součet $ G $ jednotlivých nodů, ze kterých je tvořena nejkratší možná cesta ze startovního pole do toho aktuálního
• $ H $ je odhadovaná vzdálenost od aktuálního pole do cíle.
• $ F $ je součet předchozích dvou hodnot. Výsledná cesta se skládá z nodů, které mají toto číslo nejmenší.

Pokud budete ve vzorci chtít použít i ohodnocení terénu (voda, bažiny, cesta, hory), vzorec může vypadat nějak následovně:

\[ F = \Big(H + (T + G)\Big) \]

• $ T $ zastupuje průchodnost aktuálního terénu (čim nižší hodnota, tím lepší průchodnost).

Výpočet hodnoty G⌗

Hodnota $ G $ se počítá jako součet hodnot $ G $ všech políček, kterými musíte projít, abyste se na aktuální políčko mohli dostat. Například z prvního pole ($ G = 0 $) přejdete na druhé ($ G = 5 $), třetí ($ G=10 $) atd. $ G $ aktuálního pole se vypočítá z $ G $ rodičovského node (odkud jsme na aktuální node přišli) + korekce.

Korekce diagonálního pohybu⌗

Při ohodnocování jednotlivých políček můžete narazit na jeden problém. Pokud se postavy přesunou o políčko umístěné šikmo od aktuálního, urazí větší vzdálenost, než kdyby šly vodorovně nebo svisle. Tato hodnota je přesně $ \sqrt{2} $ (=1,414213562) krát větší. Aby se nemuselo počítat s desetinnými čísly (operace s desetinnými čísly jsou obecně pomalejší než s celými čísly), zaokrouhlíme hodnotu na 1,4 a vynásobíme deseti. Vyjde nám číslo 14. To budeme přičítat při pohybu šikmo. Aby zůstalo ohodnocení vyrovnané i pro pohyb vodorovně a svisle (šikmá políčka by vždy měla podstatně větší ohodnocení a proto by se nikdy nepoužila.) bude se při tomto pohybu přičítat číslo 10.

Poznámka: Číslo deset vzniklo z poměru délky cesty vodorovně nebo svisle a délky cesty šikmo. Základní poměr je 1:1,414213562. Protože nechceme počítat s desetinnými čísly (důvod je popsán výše), zaokrouhlíme poměr na jedno desetinné číslo 1 ku 1,4 a vynásobíme 10. Vznikne poměr 10:14. Samozřejmě je možné čísla ještě vydělit dvěma (vyjdou nám čísla 5 a 7), aby nevycházela tak vysoká čísla.

Výpočet hodnoty H⌗

Hodnota $ H $ není před vytvořením finální cesty nikdy přesně známá. Proto se tato hodnota vypočítává heuresticky (=odhadem). Dopředu totiž nevíte, zda se v cestě neobjeví neprostupná skála, příliš divoká řeka nebo bezedná jáma. Pro tento výpočet existuje několik možných postupů, zde uvedu dva nejznámější.

Poznámka: Pokud by hodnota $ H $ byla rovna nule, algoritmus by se proměnil v Dijkstrův.

Manhattanská metrika⌗

Manhattanská metrika je postup, kterým lze zjistit nejkratší možnou vzdálenost z bodu $ A $ do bodu $ B $. Zjednodušený vzorec pro dva body:

\[ H = T \cdot \Big( |start.X - cil.X| + |start.Y - cil.Y| \Big) \]

$ X $ a $ Y $ jsou souřadnice startu a cíle. Podmínkou použití Manhattanské metriky je, že se pohybujete ve čtvercové síti a to jen do čtyř hlavních směrů - nahoru, doprava, dolů a doleva. Písmeno $ T $ reprezentuje nejmenší ohodnocení terénu.

Poznámka: Manhattanskou metriku je jednoduše možné použít i pro hexagonální mapu (EN). Není tedy nutné používat zrovna čtvercovou síť.

Na obrázku jsou dvě pole, start (zelené) a cíl (červené). Vzdálenost mezi těmito dvěma body Manhattanskou metrikou vypočítá následovně:

\[ H = |6 - 2| + |2 - 9| = 11 \]

Manhattanská metrika má ale jednu hlavní nevýhodu. Tou je její omezení pohybu na čtyři hlavní směry.

Chebyshevova vzdálenost (Diagonální pohyb)⌗

Pokud chcete postavám umožnit i diagonální pohyb, je potřeba vzore trochu upravit:

\[ dx = |start.x - cil.x| \] \[ dy = |start.y - cil.y| \]

\[ H = D \cdot max(dx + dy) \]

Pokud používáte korekci pro pohyb diagonálně, použijte tento vzorec:

\[ H = D_1 \cdot (dx + dy) + (D_2 - 2 * D_1) \cdot min(dx, dy) \]

Čísla $ D_1 $ a $ D_2 $ je nutné nahradit za korekci pohybu diagonálně. Např. $ D_1 = 5 $ a $ D_2 = 7 $

Vyhledávací algoritmus A*⌗

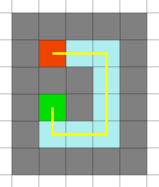
Konečně nastala ta pravá chvíle, aby jsme si ukázali, jak tento vyhledávací algoritmus funguje v akci. Začneme vybráním startovního (zelený čtvereček) a cílového (červený čtvereček) pole. Šedivá pole jsou neprostupná.

Pohyb ve čtyřech směrech⌗

Nejprve si ukážeme pohyb ve čtyřech hlavních směrech - nahoru, doprava, dolů a doleva. Jako heuristika nám v tomto případě bohatě poslouží Manhattanská metrika.

Poznámka: V tomto případě nemusíte používat opravu pro pohyb šikmo. Jako cenu přechodu tak můžeme použít číslo 1.

Prvním krokem je výpočet ohodnocení pro startovní pole.

• $ G = 0 $ – Startovní pole je první node, neušli jsme zatím žádnou cestu.
• $ H = 1 \cdot \Big( |2 - 10| + |4 – 2| \Big) = 10 $
• $ F = 0 + 10 = 10 $

Když má pole své ohodnocení, můžeme ho přidat na otevřený seznam. Z otevřeného seznamu vybereme node s nejnižším $ F $ – protože na otevřeném seznamu je aktuálně jen jeden node, je jasné, který to bude – start. Vybraný node (budeme mu pro přehlednost říkat aktuální) odebereme z otevřeného seznamu a přidáme do seznamu uzavřeného. Pro všechna sousedící pole (v našem případě jde jen o pole nad, vpravo, pod a vlevo od startu):

• Pokud je pole na uzavřeném seznamu, budeme ho ignorovat.
• Pokud je pole neprostupné, budeme ho ignorovat
• Pokud node není na otevřeném seznamu
  • Nastavte tomuto node rodiče na aktuální node (start)
  • Vypočítejte všechny hodnoty, $ G $, $ H $ a $ F $
• Pokud sousedící node již je na otevřeném seznamu
  • Zkontrolujte, zda $ G $ sousedícího node je větší než $ G $ aktuálního node + korekce.
    • Pokud hodnota $ G $ souseda je menší než $ G $ aktuálního node + korekce pro přestup z aktuálního na souseda (Například pokud soused má $ G = 20 $, aktuální node $ G = 10 $ a cena přechodu je 5, bude tato podmínka platit.
      • Nastavte rodiče souseda na aktuální node a přepočítejte všechny hodnoty ($ G $, $ H $, $ F $). Pokud udržujete otevřený seznam sežazený podle hodnty $ F $, nezapomeňte ho znovu seřadit.

S hledáním končíme když je cíl na uzavřeném seznamu (cíl byl nalezen) nebo když je otevřený seznam prázdný (cesta neexistuje). Nyní si postup demonstrujeme na obrázku:

Na obrázku se objevilo několik nových hodnot. V levém dolním rohu jsou hodnoty $ G $. V pravém dolním rohu je hodnota $ H $. Vypočítaná je pomocí Manhattanské metriky. Poslední a nejdůležitější hodnotou je $ F $, tedy celkové ohodnocení pole, která je vypsána v horním levém rohu.

Algoritmus by normálně vybral pole s nejmenší hodnotou $ F $. Zde jsou taková pole ale dvě. Které z nich vybrat? To je více-méně jedno. Obecně je rychlejší vybrat to pole, které bylo později přidané na otevřený seznam. Další možností je prohledat obě dvě možné cesty a nakonec vybrat tu kratší. Musíte ovšem počítat s vyšší časovou a paměťovou náročností.

Dejme tomu, že vybereme pole napravo od zeleného. Na šedivá pole vstoupit nelze, proto je budeme ignorovat. To samé platí pro výchozí bod (zelený čtverec), který je na uzavřeném seznamu. Zbyla nám dvě pole (nad a pod azurovým polem), pro které musíme vypočítat nové ohodnocení.

Opět nastal problém, kdy máme dvě stejně ohodnocená pole. Ještě jednou tedy vybereme později přidaný node (tedy ten nad azurovým). Po přesunu zjistíme, že všechna pole jsou buď na uzavřeném seznamu (start, azurové pole), na otevřeném seznamu (pole nad startem) nebo jde o zdi. V úvahu tak připadá jen jedno pole – to nad startem.

Protože již je na otevřeném seznamu, zkontrolujeme, jestli jeho $ G \gt G_aktualni + \text{korekce} $:

\[ 1 \lt 2 + 1 \]

To samozřejmě platí, proto budeme pokračovat, aniž bychom něco měnili. Konečně tedy náš algoritmus nalezl (už od pohledu jasně viditelný) správný směr. Následující postup bude jen opakování již popsaného.

Pohyb ve více směrech⌗

Rozdílů oproti pohybu do čtyř stran je jen několik. Zaprvé, jako heuristika se používá Chebyshevova vzdálenost. Ta vrací lepší výsledky. Zadruhé, je dobré použít korekci pro pohyb diagonálně.

Nevýhody A*⌗

Stejně tak jako cokoli jiného, i A* pathfinding není dokonalý a má své mouchy. Na velkých mapách může algoritmus vyžadovat velké množství položek v uzavřeném (closed list) i otevřeném (opened list) seznamu. Jejich uložení může zabrat příliš místa, obzvláště, pokud se hledá několik cest souběžně. I kdyby bylo dostatek místa pro uložení, práce s jednotlivými seznamy může být kvůli velkému množství položek neefektivní.